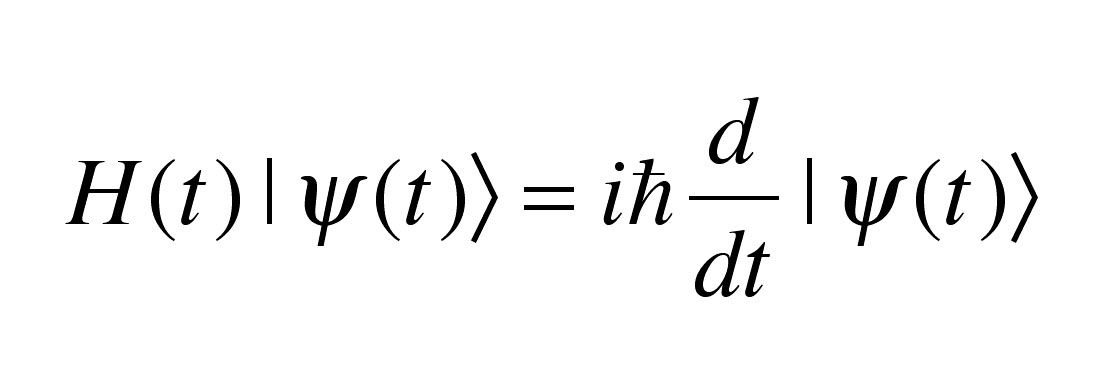This is now referred to as the radial wave equation, and would be identical to the one-dimensional Schr odinger equation were it not for the term /r 2 added to V, which pushes the particle away. which you have also implicitly used in your derivation for 2. The equation for Rcan be simpli ed in form by substituting u(r) rR(r): 2 2m d2u dr2 + ' V+ 2 2m l(l+ 1) r2 u Eu with normalization R drjuj2 1. Other authors making similar claims in that same year Johann Kudar, Théophile de Donder and Frans-H. I am trying to reconcile two different ways of producing the Schrödinger equation in momentum space starting from the Schrödinger equation in abstract notation. Vladimir Fock also discovered the equation independently in 1926 slightly after Klein's work, in that Klein's paper was received on 28 April 1926, Fock's paper was received on 30 July 1926 and Gordon's paper on 29 September 1926. The equation was named after the physicists Oskar Klein and Walter Gordon, who in 1926 proposed that it describes relativistic electrons. It is a quantized version of the relativistic energy–momentum relation E 2 = ( p c ) 2 + ( m 0 c 2 ) 2. It is second-order in space and time and manifestly Lorentz-covariant. ( Newton's dot notation for the time derivative is used.) The Schrdinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. The Klein–Gordon equation ( Klein–Fock–Gordon equation or sometimes Klein–Gordon–Fock equation) is a relativistic wave equation, related to the Schrödinger equation. Schrdinger's equation inscribed on the gravestone of Annemarie and Erwin Schrdinger.